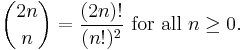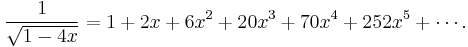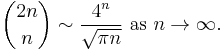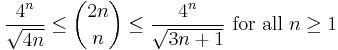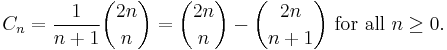Central binomial coefficient

In mathematics the nth central binomial coefficient is defined in terms of the binomial coefficient by

{2n \choose n} = \frac{(2n)!}{(n!)^2}\text{ for all }n \geq 0.

They are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle. The first few central binomial coefficients starting at n = 0 are:

1, 2, 6, 20, 70, 252, 924, 3432, 12870, 48620, … (sequence A000984 in OEIS)

Properties

These numbers have the generating function

\frac{1}{\sqrt{1-4x}} = 1 %2B 2x %2B 6x^2 %2B 20x^3 %2B 70x^4 %2B 252x^5 %2B \cdots.

By Stirling's formula we have

{2n \choose n} \sim \frac{4^n}{\sqrt{\pi n}}\text{ as }n\rightarrow\infty.

Some useful bounds are

\frac{4^n}{\sqrt{4n}} \leq {2n \choose n} \leq \frac{4^n}{\sqrt{3n%2B1}}\text{ for all }n \geq 1

and, if more accuracy is required,

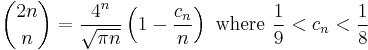{2n \choose n} = \frac{4^n}{\sqrt{\pi n}}\left(1-\frac{c_n}{n}\right)\text{ where }\frac{1}{9} < c_n < \frac{1}{8} for all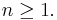 n \geq 1.

The closely related Catalan numbers Cn are given by:

C_n = \frac{1}{n%2B1} {2n \choose n} = {2n \choose n} - {2n \choose n%2B1}\text{ for all }n \geq 0.

A slight generalization of central binomial coefficients is to take them as 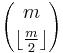{ m \choose {\lfloor \frac{m}{2} \rfloor} } and so the former definition is a particular case when m = 2n, that is, when m is even.

See also

External links

This article incorporates material from Central binomial coefficient on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.